Le Insidie nei Dati e nei Grafici
Ogni giorno sui giornali appaiono articoli che citano studi che parlano di statistiche, evidenze, che dimostrano relazioni. Spesso però, dati e grafici possono essere ingannevoli: possono essere omessi, manipolati, abbelliti, più o meno intenzionalmente, specialmente se l’intento è quello di convincere l’interlocutore. Possono evidenziare effetti e relazioni tra variabili che in realtà non esistono o che, se esistono, sono più deboli di quanto supposto. Spesso vengono anche presentati in modo da far leva sul bisogno di ciascuno di confermare le proprie convinzioni.
Abbiamo raccolto in ordine sparso delle piccole trappole in cui si può incappare leggendo dei dati o guardando un grafico, con delle piccole accortezze che è bene avere per non caderne vittima:
- Post Hoc - Uno degli errori più comuni è quello del “post hoc” (dal latino “post hoc, ergo propter hoc”, ossia “dopo di questo, quindi a causa di questo”): esso consiste nell’inferire che un evento sia la causa di un altro solo perché lo precede. In questo caso credo sia giusto parlare di tentazione più che di errore, dal momento che è una tendenza legittima quella di cercare di trovare cause chiare ad eventi rilevanti. Un esempio lampante è quello dell’andamento dei mercati o del PIL dopo l’insediamento del governo. Il mercato sale, si celebra l’efficacia delle riforme, il mercato scende, si addita l’inettitudine del governo. Spesso invece, le cause sono meno chiare ed è probabile che le spiegazioni siano parziali e non ben definite. Si fa quel che si può.
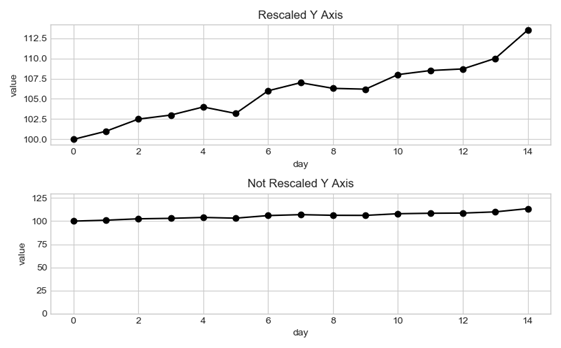
- Assi - Uno dei modi più semplici per esagerare o sminuire l’andamento di una variabile è quello di giocare con gli assi del grafico. I metodi sono principalmente due: troncare gli assi e utilizzare l’asse secondario. Troncando l’asse delle y, ad esempio, si può far credere che una quantità si muova molto di più (o molto di meno) di quanto effettivamente faccia. Guardate i due grafici sotto: aumento deciso nel primo grafico e calma piatta nel secondo, ma le due serie sono le stesse. È solo la scala che cambia. E l’enfasi che si vuole porre sul fenomeno.
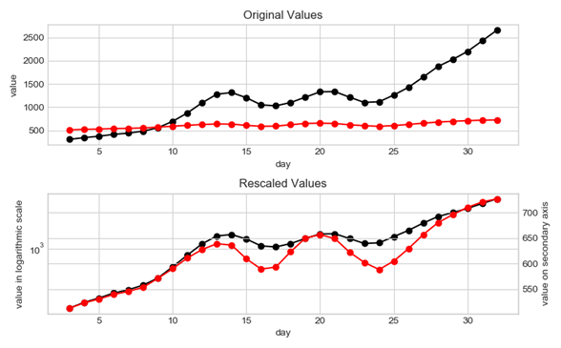
Utilizzare l’asse secondario spinge invece chi guarda a mettere in relazione due variabili e forza a supporre una relazione fra le due. Nei due grafici sotto sono rappresentate le stesse due variabili; solo che al secondo grafico è stato fatto un po’ di maquillage: un asse in scala logaritmica di qua, un asse secondario di là, e abbiamo indotto chi guarda a credere che ci sia una chiara relazione tra le due serie storiche. Di solito gli assi sono la smoking gun quando si tratta di sottolineare o sminuire un fenomeno.
- Media e mediana - La confusione tra queste due quantità è uno dei grandi classici dell’illusionismo statistico. Se 999 persone guadagnano 10 euro l’anno, mentre una persona ne guadagna un milione, sarebbe fuorviante far notare che il gruppo di 1000 persone guadagna in media 1000 euro a testa. Come sarebbe poco saggio attraversare un fiume che in media è profondo un metro. Per alcune variabili citare la media è fuori luogo; spesso la mediana è una quantità più robusta e veritiera.
- Grafici a torta - I grafici a torta, se presi isolatamente, nascono due diversi tipi di insidie: in primis, tralasciano il dato in valore assoluto. Secondo, possono spingere l’osservatore ad assumere che la torta, intesa come ammontare totale da dividere, rimanga fissa. Questo equivoco è alla base delle retoriche più fastidiose, dove ognuno può guadagnare solo a spese dell’altro. L’economia non è un gioco a somma zero, e spesso i grafici a torta alimentano l’equivoco. E non sono i soli: quando qualcuno ci cita la regola paretiana secondo cui il 20% più ricco della popolazione detiene l’80% della ricchezza, l’indignazione (per alcuni) che ne consegue spesso ostruisce la domanda più importante, ossia: c’è “ricambio” tra l’80% e il 20%? Quanti di quelli che appartenevano all’80% sono ora nel 20%? Magari, un paese con meno sperequazione può essere un paese più ingessato. Le “torte” spesso nascondono le dinamiche dei fenomeni.
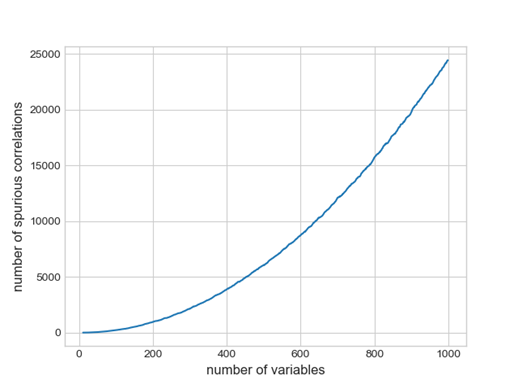
- Correlazione - La correlazione è una delle metriche più (ab)usate e più mal interpretate. La prima comune osservazione è che l’indice di correlazione più comune (indice di correlazione di Pearson) è un indice di correlazione lineare: spesso le relazioni ci sono, ma sono più complesse di quelle lineari. In secondo luogo, quasi mai nei vari studi le correlazioni vengono accompagnate da degli intervalli di confidenza, che darebbero un grado di incertezza sul valore in questione. Per finire, una nota di cautela per quanto riguarda le correlazioni deve essere utilizzata quando se ne parla nell’ambito dei big data: all’aumentare delle variabili, il numero di correlazioni spurie (o false) aumenta più che proporzionalmente.
- Campionamento - I problemi sulle correlazioni affondano le loro radici in quello che costituisce il fondamento della statistica, ossia il campionamento: se la scienza sta affrontando una "crisi di riproducibilità", in cui i due terzi dei ricercatori hanno tentato e fallito nel riprodurre gli esperimenti di un altro ricercatore [1], lo si deve soprattutto a problemi di campionamento (sampling bias). Ricordarsi dunque di prendere sempre con le pinze lo studio dell’Università del Connecticut che mette in relazione la fertilità con il consumo di thè.
[1] Most scientists 'can't replicate studies by their peers' di Tom Feilden (https://www.bbc.com/news/science-environment-39054778).
[2] Gran parte di questo articolo prende spunto da un classico di Darrell Huff, ‘How to Lie With Statistics’.



